What is pressure in fluids, and how does it affect engineering problems?
In our previous articles, we looked at how to use various principles, such as moments of force, to solve engineering problems. In this article, we’re going to look into principles of fluids and how they affect engineering problems.
Pressure due to height of a fluid
We can calculate the pressure exerted by a fluid at any given depth. Imagine a ‘tower’ of fluid above the point at which we want to measure. We will have the weight of this column of fluid acting on a point. The pressure, p, at a given depth can be calculated using the equation:
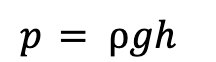
In this equation:
- p = pressure (Pa)
- ρ = density of the fluid (greek letter Rho, not to be confused with ‘p’ for pressure) (kg/m3)
- g = Gravitational acceleration (taken as 9.8m/s2 on Earth). (m/s2)
- h = The height of fluid above the point (depth of the point) (m)
Real life examples
Let’s have a look at some real life examples to see how this works. Firstly, let’s calculate the hydrostatic pressure exerted on a diver when they reach a depth of 30m. Take the density of water is 1000 kg/m³, and acceleration due to gravity is 9.8 m/s². Using the equation above, the pressure is 294 kPA.
Say we wanted to calculate the hydrostatic pressure exerted at the bottom of the Mariana trench, which is the deepest point in the earth’s ocean. Density of seawater is 1020 kg/m³, and acceleration due to gravity is 9.8 m/s². The depth of the Mariana trench is 11,034m! If we give our answer in units of bar, using the equation above we get 1,103bar.
Absolute pressure vs Gauge pressure
Air is a fluid, and it can also apply to pressure. This pressure of the air at sea level can be calculated as roughly 100kPA, which is also known as 1bar. This pressure is referred to as standard atmospheric pressure.
For context, the density of air at sea level is approximately 1.225 kg/m³, and it gradually reduces to 0 kg/m³ as we move to outer space.
Now, during our calculations above, we didn’t take into account this ‘additional’ pressure that is already present because of the atmosphere. It’s important to recognise the difference between these two terms:
- Absolute Pressure – this is the total pressure above that of a complete vacuum, in other words, total above zero pressure.
- Gauge Pressure – the pressure above that which is already present because of the atmosphere.
So, absolute pressure = gauge pressure + atmospheric pressure. If we look at our first real life example calculation from above, we can see that we were actually calculating the gauge pressure on the diver.
Let’s redo that calculation, rewording it slightly. Now we’re going to calculate both the gauge and absolute pressure exerted on a diver when reaching a depth of 30m. Again, the density of water is 1000 kg/m³, and acceleration due to gravity is 9.8 m/s². Atmospheric pressure is 101 kPa.
Using the original equation we saw right at the start of our article, we can calculate the gauge pressure as 294 kPa and the absolute pressure as 395 kPa.
Keep an eye out for our next article looking into how heat can affect engineering problems.
Interested in our courses?
You can read more about our selection of accredited online mechanical, electrical, civil and aerospace engineering courses here.
Check out individual courses pages below:
Diploma in Aerospace Structures
Diploma in Principles of Flight
Diploma in Aerodynamics, Propulsion and Space
Higher International Diploma in Mechanical Engineering
Higher International Certificate in Mechanical Engineering
Diploma in Mechanical Engineering
Diploma in Mechanical Technology
Alternatively, you can view all our online engineering courses here.
Recent Posts
A Quick Guide to Thermal Stress
A Quick Guide to Thermal Stress Thermal expansion and the resulting thermal stress are key concepts in engineering and physics. They describe how materials expand or contract when exposed to temperature changes. Understanding these principles is essential for designing structures and systems that can withstand environmental fluctuations without failure. What is Thermal Expansion? When materials […]
How to Calculate Shear Stress
Introduction to Shear Force and Shear Stress Shear force and shear stress are critical concepts in mechanics and materials science, often encountered in structural engineering and manufacturing. Shear Force refers to the internal force in a material that acts parallel to its cross-section. It is measured in Newtons (N). Shear force arises when two opposing […]
Kirchhoff’s current and voltage laws
Kirchhoff’s current and voltage laws In our last article, we looked at the principles and operation of a d.c motor. In this article, we’re going to investigate Kirchoff’s current and voltage laws, as well as how to apply them to engineering problems. Kirchoff’s law of current Kirchoff’s law of current states that the algebraic sum […]

