What is Bernoulli’s principle?
In our previous article, we looked at ideal gas laws and how they can be used in engineering problems. In this article we’re going to look into Bernoulli’s principle and how it can affect engineering problems.
Bernoulli’s principle
Bernoulli’s principle is a fundamental law governing the motion of fluids. It relates an increase in flow velocity to a decrease in pressure. Let’s look at an example. For the same volume of air at the entry to the tube below to pass through the narrower section, the air has to speed up.
Based on Newton’s theory that energy can’t be created or destroyed, just transferred, the increased speed has to have a corresponding decrease in pressure. As the air exits the narrow section, it slows and regains its original pressure.
We can explain this using a familiar situation. Imagine you’re driving at speed on a motorway. If you open the window slightly, you can feel a rush of air entering. The air going by the window has to speed up to get out of the way of the car. When air speeds up, it loses pressure. The lower pressure of the air speeding past the window sucks more air out of the window, increasing flow into the car through the vents, to replace the lost air.
Bernoulli’s Equation.
The Bernoulli equation states
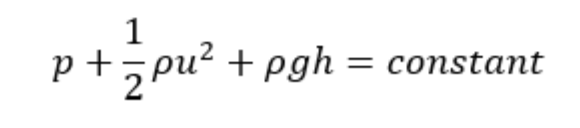
Where p is the pressure (Pa), ρ is the density (kg/m3), u is the flow velocity (m/s), g is the acceleration due to gravity (9.81 m/s2) and h is the height from some datum (m).
It can also be written as:
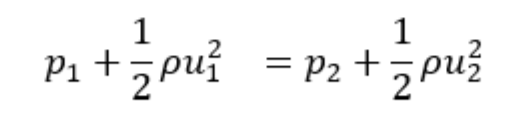
Where points 1 and 2 lie on a streamline at the same height from some datum the fluid has constant density, i.e. incompressible (ρ1=ρ2) the flow is steady, and there is no friction.
Although these restrictions sound severe, the Bernoulli equation is very useful, partly because it is very simple to use and partly because it can give great insight into the balance between pressure, velocity and elevation.
Pressure/velocity variation
Let’s consider the steady flow of a constant density fluid in a converging duct, without losses due to friction as shown below. The flow satisfies all the restrictions governing the use of Bernoulli’s equation. Upstream and downstream of the contraction, we make the assumption that the velocity is constant over the inlet and outlet areas and parallel.
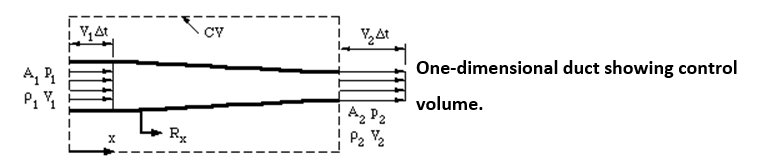
When streamlines are parallel the pressure is constant across them, except for hydrostatic head differences (if the pressure was higher in the middle of the duct, for example, we would expect the streamlines to diverge, and vice versa).
If we ignore gravity, then the pressures over the inlet and outlet areas are constant. Along a streamline on the centerline, the Bernoulli equation and the one-dimensional continuity equation give, respectively,
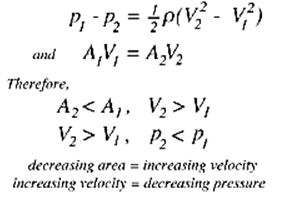
When air flows from a region of high pressure to one at a lower pressure, the pressure difference provides a force in the direction of flow, and the air therefore accelerates. Conversely, flow from a low pressure to a higher one results in a decrease in speed. The image below shows this using the example of a car driving.
Keep an eye out for our next article looking into engineering materials and their atomic structure
Interested in our courses?
You can read more about our selection of accredited online mechanical, electrical, civil and aerospace engineering courses here.
Check out individual courses pages below:
Diploma in Aerospace Structures
Diploma in Principles of Flight
Diploma in Aerodynamics, Propulsion and Space
Higher International Diploma in Mechanical Engineering
Higher International Certificate in Mechanical Engineering
Diploma in Mechanical Engineering
Diploma in Mechanical Technology
Alternatively, you can view all our online engineering courses here.
Recent Posts
A Quick Guide to Thermal Stress
A Quick Guide to Thermal Stress Thermal expansion and the resulting thermal stress are key concepts in engineering and physics. They describe how materials expand or contract when exposed to temperature changes. Understanding these principles is essential for designing structures and systems that can withstand environmental fluctuations without failure. What is Thermal Expansion? When materials […]
How to Calculate Shear Stress
Introduction to Shear Force and Shear Stress Shear force and shear stress are critical concepts in mechanics and materials science, often encountered in structural engineering and manufacturing. Shear Force refers to the internal force in a material that acts parallel to its cross-section. It is measured in Newtons (N). Shear force arises when two opposing […]
Kirchhoff’s current and voltage laws
Kirchhoff’s current and voltage laws In our last article, we looked at the principles and operation of a d.c motor. In this article, we’re going to investigate Kirchoff’s current and voltage laws, as well as how to apply them to engineering problems. Kirchoff’s law of current Kirchoff’s law of current states that the algebraic sum […]

