What are ideal gas laws?
In our previous article, we looked at how continuity can affect engineering problems. In this article, we’re going to look into what ideal gas laws are and how they can affect engineering problems.
What are ideal gas laws?
Ideal gas laws are a set of laws and equations that govern the relationship between the pressure, volume, and temperature of a gas.
For an engineer, ideal gas laws are very important in the design of many items. For example, the pressure of gas inside a tank will have an impact on the design of pressure vessels for transportation, or the working temperature of a gas turbine engine. We’re going to check out these laws below
Boyle’s Law
Boyle’s law states that the volume, V, of a fixed mass of gas is inversely proportional to its absolute pressure, p, at constant temperature:
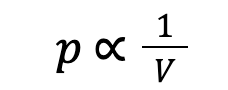
We could rewrite this as:
Where p = pressure (Pa), V = volume of the gas (m³), and k = a constant.
The actual quantity of ‘k’ isn’t important. It’s important that for a given gas it’s constant, and so the relationship of volume to pressure is inversely proportional for a constant temperature. Therefore for a change in pressure, say from P1, to P2, you get a corresponding change in volume, from V1, to V2. As k is a constant, we therefore know that:
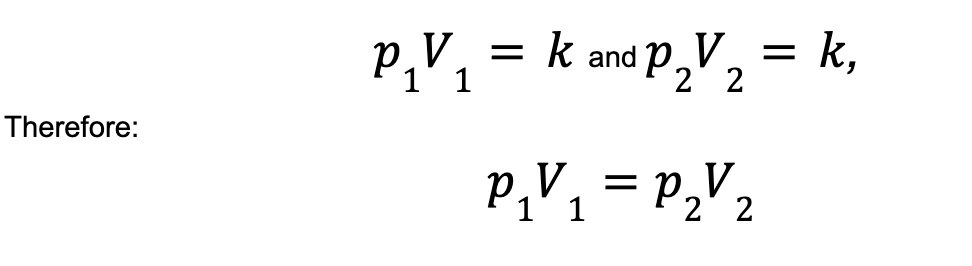
Charles’ Law
In Boyle’s law, we saw the relationship between an ideal gas’s volume and pressure. Charles’ law gives a similar relationship, but this time it’s between an ideal gas’s temperature and pressure. Charles’ law states that for a given mass of gas at constant temperature, the volume V is directly proportional to its thermodynamic temperature T:
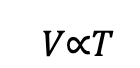
We can rewrite it to introduce a constant:
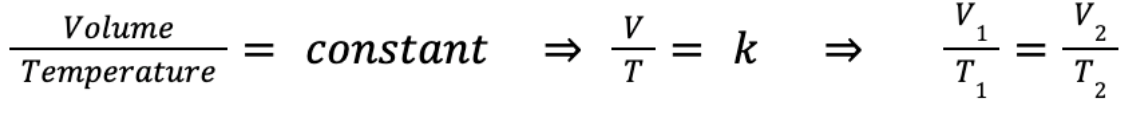
Where V = volume (m³), T = temperature (K) and k is again a constant. V₁ and T₁ are the starting volume (m³) and temperature (K), and V₂ and T₂ are the final temperature and pressure, for a fixed pressure. This is true for any given pressure, as long as it remains constant.
Gay-Lussac’s Law
Now we know that for an ideal gas, there is a relationship between volume and pressure (Boyle’s law), and a relationship between volume and temperature (Charles’ law). So it stands to reason that there must be a relationship between pressure and temperature!
Given the above, this would be easy to derive, and it results in something called the Gay-Lessac’s law. The pressure p of a fixed mass of gas is directly proportional to its thermodynamic temperature, T, at a constant volume:
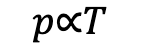
If we do a similar arrangement as we’ve done before, we know this can be rearranged as:
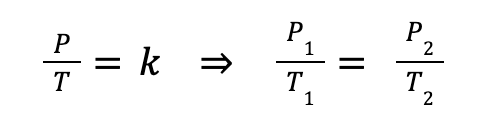
Where P1 and T1 are the starting pressure (Pa) and temperature (K), and P2 and T2 are the final temperature and pressure, for a fixed volume.
Dalton’s law of partial pressure
The final part of the ideal gas law is called Dalton’s law of partial pressure, and it simply states that the total pressure of a mixture of gases occupying a given volume is equal to the sum of the pressures of each gas, considered separately, at constant temperature.
While it might sound complicated, what it means is that for a container which has a mixture of different gases in it, the total pressure in the container is the sum of each individual gas pressure added up (assuming a constant temperature):
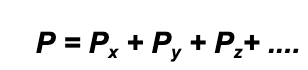
Where P = total pressure, Px is pressure by gas X, Py is the pressure by gas Y etc. A partial pressure is the individual pressure of a single gas within that mixture.
Keep an eye out for our next article looking into Bernoulli’s principle and how we can apply it to engineering problems.
Interested in our courses?
You can read more about our selection of accredited online mechanical, electrical, civil and aerospace engineering courses here.
Check out individual courses pages below:
Diploma in Aerospace Structures
Diploma in Principles of Flight
Diploma in Aerodynamics, Propulsion and Space
Higher International Diploma in Mechanical Engineering
Higher International Certificate in Mechanical Engineering
Diploma in Mechanical Engineering
Diploma in Mechanical Technology
Alternatively, you can view all our online engineering courses here.
Recent Posts
A Quick Guide to Thermal Stress
A Quick Guide to Thermal Stress Thermal expansion and the resulting thermal stress are key concepts in engineering and physics. They describe how materials expand or contract when exposed to temperature changes. Understanding these principles is essential for designing structures and systems that can withstand environmental fluctuations without failure. What is Thermal Expansion? When materials […]
How to Calculate Shear Stress
Introduction to Shear Force and Shear Stress Shear force and shear stress are critical concepts in mechanics and materials science, often encountered in structural engineering and manufacturing. Shear Force refers to the internal force in a material that acts parallel to its cross-section. It is measured in Newtons (N). Shear force arises when two opposing […]
Kirchhoff’s current and voltage laws
Kirchhoff’s current and voltage laws In our last article, we looked at the principles and operation of a d.c motor. In this article, we’re going to investigate Kirchoff’s current and voltage laws, as well as how to apply them to engineering problems. Kirchoff’s law of current Kirchoff’s law of current states that the algebraic sum […]