How Motion in a Circle Affects System Dynamics
In engineering applications, circular motion is encountered in various systems such as rotating machinery, turbines, gears, flywheels, and vehicle dynamics. Unlike linear motion, circular motion involves continuously changing direction, resulting in dynamic effects that must be analysed to ensure safe and efficient design.
Understanding these dynamics is essential for designing mechanical systems subjected to rotational or curved motion, where unbalanced forces or vibrations can lead to mechanical failure or reduced performance.
Examples of circular motion include:
- an artificial satellite orbiting the Earth at a constant height,
- a stone which is tied to a rope and is being swung in circles,
- a car turning through a curve in a racetrack,
- a gear turning inside a mechanism
- a motor vehicle wheel.
Consider a body moving in a circular path with a constant angular velocity, as follows:
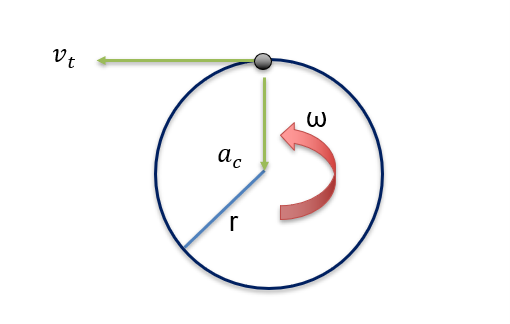
The angular velocity, ω, is defined as the rate of change of angle,θ , with respect to time, t, and is analogous to its linear velocity counterpart:
Linear Velocity v (m/s) = ∆x⁄∆t
Angular Velocity ω (rad/s) = ∆θ⁄∆t
Constant Angular Velocity
At any given instant in time, t, there will be a tangential velocity, vt, which is perpendicular (at right angles to) the radius, r of the circle, which is defined as:
vt = ω r
The above equation is the ‘link’ between the linear and the angular domain.
Even though we are considering constant angular velocity, there will be an acceleration towards the centre of the circle, ac. This acceleration is known as the centripetal acceleration.
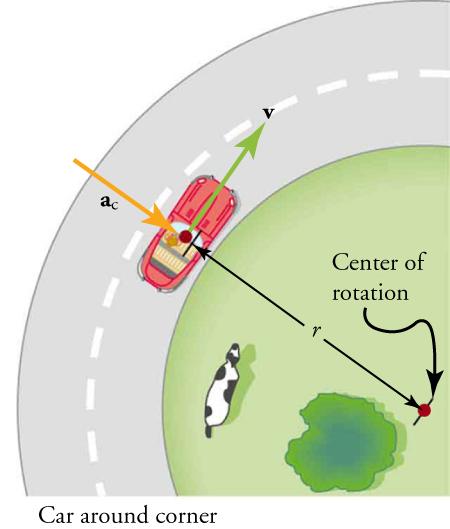
Consider a vehicle travelling around a bend which forms part of a circle. As you are probably aware, you, as a passenger of such a vehicle, will experience a tendency to feel like you are being forced out towards the outside of the circle. This is the reaction force associated with the centripetal acceleration and is known as the centrifugal force due to the centrifugal acceleration. The centripetal acceleration (and its associated centripetal force) is always towards the centre of the circle and it is the job of the tyres on the vehicle and the chassis stiffness to produce this force as this is the force that holds the vehicle in a circular path.
The centripetal acceleration is given by:
ac = vt2⁄r
By Newton’s second law, the associated centripetal force is
Fc = mac
Fc = mvt2⁄r
Example 1
A vehicle of mass 1250 kg travels round a bend of radius 75 m, at 60 km/h. Determine the centripetal force acting on the vehicle.
First, convert the velocity to SI units:
60km/hr = 60,000 m /hr = 60,000 / 3600 m/s = 16.7 m/s
Fc = mv2⁄r
Fc = (1250)(16.7)2⁄75
Fc = 4630N
Changing Angular Velocity
In this case, the angular velocity is changing, and hence we will also have an angular acceleration, α.
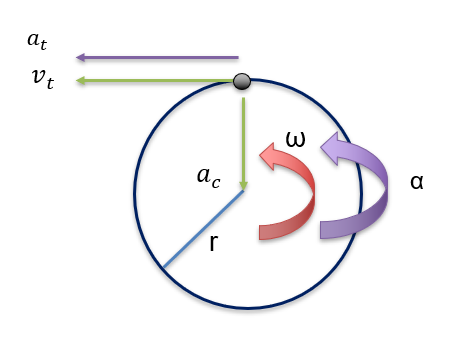
Linear Velocity v (m/s) = ∆x⁄∆t
Angular Velocity ω (rad/s) = ∆θ⁄∆t
Linear Acceleration, at (m/s2) = Δv⁄∆t
Angular Acceleration, α (rad/s2) = ∆ω⁄∆t
There will also be a tangential acceleration, at, given by:
at = α r
Example 2
A 5kg wheel with a radius of 300mm accelerates from rest to 500 RPM in 10 seconds. At time, t = 10s, determine
a) the angular velocity,
b) the angular acceleration
c) the tangential velocity on the rim of the wheel
d) the centripetal acceleration and centripetal force
e) the tangential acceleration
Solutions
a) angular velocity
ω = 500 RPM
ω = 500⁄60 rev per sec = 500⁄60 (2π) rad/s
ω = 52.4 rad/s
b) angular acceleration
α = Δω⁄Δt = (52.4-0)⁄(10-0) = 5.24 rad/s2
c) tangential velocity
vt = ω r = (52.4)(0.3) = 15.7 m/s
d) centripetal acceleration and force
ac = vt2⁄r = (15.7)2⁄0.3 = 822.5 m/s2
Fc = mac = (5)(822.5) = 4112.3N = 4.1kN
e) tangential acceleration
at = α r
at = (5.24) (0.3) = 1.6 rad/s2
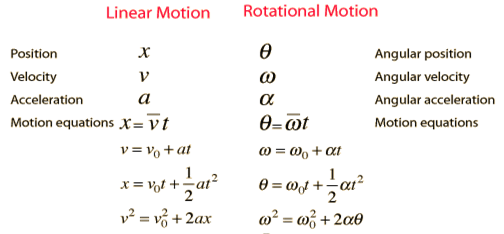
It should also be noted that all of the linear equations of motion for constant acceleration (SUVAT) have their angular motion equivalents as summarised below:
Interested in our engineering courses?
We have over 70 courses across all major engineering disciplines, including, mechanical, electrical and electronic, civil, aerospace, industrial, computer and general engineering. Visit our course catalogue for a complete list of fully accredited engineering programmes.
A small selection of short courses …
Diploma in Mechanical Engineering
Diploma in Structural Engineering
Level 6 Courses
International Graduate Diploma in Mechanical Engineering
International Graduate Diploma in Civil Engineering
International Graduate Diploma in Aerospace Engineering
Level 5 Courses
Higher International Diploma in Mechanical Engineering
Higher International Diploma in Civil Engineering
Higher International Diploma in Aerospace Engineering
Level 4 Courses
Higher International Certificate in Mechanical Engineering
Higher International Certificate in Civil Engineering
Higher International Certificate in Aerospace Engineering
Alternatively, you can view all our online engineering courses here.
<
Recent Posts
Starting Your Engineering Journey: The Higher International Certificate (Level 4)
Starting Your Engineering Journey: The Higher International Certificate (Level 4) Embarking on a career in engineering is a significant decision, and choosing the right starting point can make all the difference. The Higher International Certificate (HIC) from iLearn Engineering® offers a flexible, accessible, and globally recognised route into the profession. Whether you are beginning your […]
Understanding Qualification Levels and Credits: a guide for engineering students
Understanding Qualification Levels and Credits: a guide for engineering students 1. Introduction to Qualification Levels 2. What Are Credits and Why Do They Matter? While 120 credits is broadly equivalent to one academic year, in traditional university settings this would usually be delivered across approximately 39 weeks with fixed timetables. In contrast, asynchronous learning models—such […]
What is Inertia and how to Calculate it ?
What is Inertia and how to Calculate it ? Inertia is the property of matter that causes it to resist changes in its velocity. This includes changes to the object’s speed or direction of motion. Inertia is directly related to mass, the greater the mass, the greater the inertia. In simple terms: “An object in […]

