How to calculate stress for direct loading of components.
If a rubber strip is pulled it stretches, and the more you pull it the more it stretches. There’s a relationship between the extension and the force applied, known as Hooke’s Law, and it can be expressed as a force extension graph:
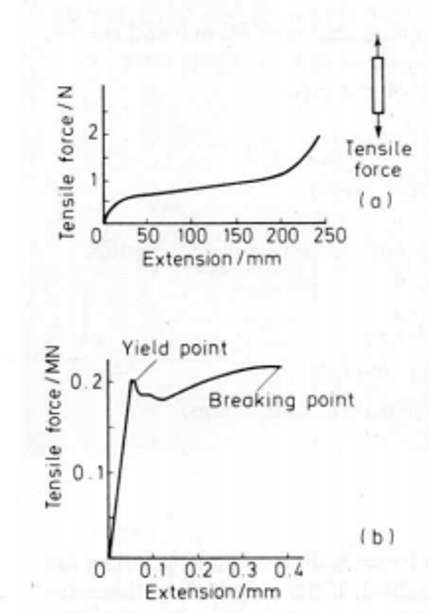
The top graph above shows the graph we’d see for a strip of rubber, and the bottom graph shows a piece of steel. You’ll notice that the forces needed to stretch steel are considerably greater than for rubber. We can also see, from looking at the extension axis, that the amount by which rubber changes length is greater than that of steel.
You can also see that the overall shapes of the graphs are very different. The rubber, after a small force, needed very little increase in force to produce greater extensions. After an extension of about 200 millimeters, the rubber becomes much more difficult to stretch. The steel needs quite large forces to produce any extension. However, when the force reaches 0.2 MN (0.2 x 106), the steel increases considerably in length without any more force being applied. The steel is said to have yielded.
Force Applied Calculation
The force is applied to the rubber and the steel strips, resulting in an increase in the lengths of the strips. The forces are said to be tensile forces and the strips are in tension. If the cross-sectional area of the strip is doubled, then twice the forces are needed to give the same extension. If the cross-sectional area is 3 times larger, then the force must be three times larger to get the same extension. For the same extension, the force per unit area should be constant. This quantity is called stress:
stress=force area
σ=FA
Where F is the force (N) and A is the area (m2). The units of stress are N/m2 or Pa (1 Pascal = 1N/ m2).
Direct or Normal Stress.
Look at the image below, with a bar of length L. Constant cross-sectional area A is subjected to an axial tensile force F.
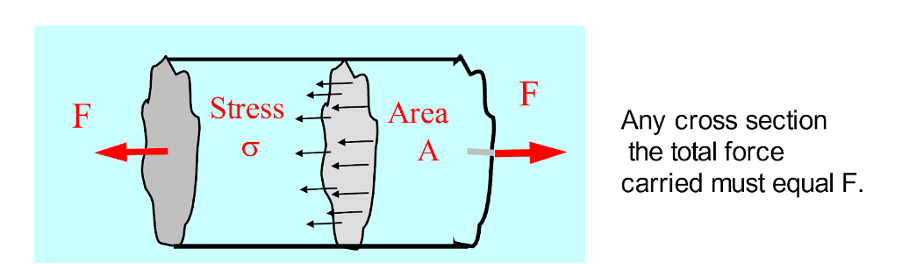
When the force is uniformly distributed over the section, then:
The stress is said to be direct stress when the area being stressed is at right angles to the line of action of the force, as is the case as shown with the rubber graph above.
Let’s look at an example. A specimen with a cross-sectional area of 50mm2 was subjected to a tensile force of 0.1 MN. We’re going to calculate the stress induced in this specimen.
Firstly, we convert the values to SI units:
1mm2 = 0.001 x 0.001m2 = 1 x 10 – 6m2
Therefore, 50mm2 = 50 x 10 = 6m2
σ=FA=0.1x10650x10-6=2×109=2GPa
Keep an eye out for more of our articles where we dive deeper into some of these concepts.
Interested in our courses?
Interested in civil or mechanical engineering? Find out more about all the civil engineering courses we have available by clicking here, and the mechanical engineering courses by clicking here.
Diploma in Mechanical Engineering
Diploma in Mechanical Technology
Diploma in Sustainable Construction
Diploma in Structural Engineering
Diploma in Building and Construction Engineering
Higher International Certificate in Civil Engineering
Higher International Diploma in Civil Engineering
Higher International Diploma in Mechanical Engineering
Higher International Certificate in Mechanical Engineering
Alternatively, you can view all our online engineering courses here.
Recent Posts
What are the principles of operation of electrical cells?
What are the principles of operation of electrical cells? In our last article, we looked at the basic electrical parameters in D.C. circuits. In this article, we’re going to move on to the principles of operation of electrical cells. We’ll look at the different types of cells and batteries, their mechanisms, and their applications. What […]
How can we calculate basic electrical parameters?
How can we calculate basic electrical parameters? In our last article, we looked at how we can select the best engineering material for the task. In this article, we’re going to move on to basic electrical parameters in D.C. circuits. As an engineer, we need to be able to define these key terms and apply […]
How can we select engineering materials?
How can we select engineering materials? In our previous article, we looked at elastic and magnetic hysteresis. In this article, we’re going to look at how we can select engineering materials. In other articles, we have previously looked at the different materials and their properties. However, it’s important that engineers understand how we can go […]